-
[알고리즘] HW2 TSP 쌩노가다 코딩.. 이틀밤낮이 흘렀다...정리필요2 2007. 10. 1. 15:39
● 알고리즘 3.11의 구현
[문제]
- 알고리즘 3.11의 TSP 문제에 대한 알고리즘을
프로그램으로 구현
- path를 출력하는 알고리즘을 개발하여 추가
[목표]
- input graph에 대한 최적 tour와 그 길이를 출력
- 연습용 input graph은 그림 3.16과
130쪽 문제5의 그림을 각각 적용
- 다른 graph들도 적용하여 결과를 확인
[힌트]
- vertex 번호는 0부터 n-1까지로 사용
- vertex subset {v2, v0}의 번호는 5 (00101)로
표현하여 이진수로는 포함되는 vertex 번호와
일치하는 bit를 1로 표시하는 방법을 적용해본다.
● Brute Force 알고리즘으로도 구현해보고,
서로 시간복잡도를 비교/분석 해본다.
::알고리즘 3.11::
void travel(int n, const number W[][],
index P[][], number& minlength) {
index i, j, k;
number D[1..n][subset of V-{v1}];
for(i=2; i<=n; i++)
D[i][Æ] = W[i][1];
for(k=1; k<= n-2; k++)
for(all subsets AÍV-{v1} containing k vertices)
for(i such that i¹1 and vi is not in A){
D[i][A] = min(j:vjÎA)(W[i][j]+D[j][A-{vj}]);
P[i][A] = value of j that gave the minimum;
}D[1][V-{v1}] = min(2£j£n)(W[1][j]+D[j][A-{v1,vj}]);
P[1][V-{v1}] = value of j that gave the minimum;
minlength = D[1][V-{v1}]
}
예를들어 해보자..
V = { v0, v1, v2, v3 }
W에서 D를 채워간다.
int W[4][4] = {
{ 0, 2, 9, INFINITY},
{ 1, 0, 6, 4},
{ INFINITY, 7, 0, 8},
{ 6, 3, INFINITY, 0} };
아무것도 거쳐가지 않고 갈때
D[v1][0] = W[0][1] = 1
D[v2][0] = W[0][2] = INFINITY
D[v3][0] = W[0][3] = 6
k = 1 하나만 거쳐서 갈 때
D[v1][v2] = min( W[1][j] + D[vj][{v2} - {vj}] ) = W[1][2] + D[v2][0] = 6 + INFINITY
D[v1][v3] = min( W[1][j] + D[vj][{v3} - {vj}] ) = W[1][3] + D[v3][0] = 4 + 6 = 10
D[v2][v1] = min( W[2][j] + D[vj][{v1} - {vj}] ) = W[2][1] + D[v1][0] = 7 + 1 = 8
D[v2][v3] = min( W[2][j] + D[vj][{v3} - {vj}] ) = W[2][3] + D[v3][0] = 8 + 6 = 14
D[v3][v1] = min( W[3][j] + D[vj][{v1} - {vj}] ) = W[3][1] + D[v1][0] = 3 + 1 = 4
D[v3][v2] = min( W[3][j] + D[vj][{v2} - {vj}] ) = W[3][2] + D[v2][0] = INFINITY + INFINITY
k = 2 두개 거쳐갈 때
D[v1][{v2, v3}] = min( W[1][j] + D[vj][{v2, v3} - {vj}] )
= min( W[1][2] + D[v2][{v3}], W[1][3] + D[v3][{v2}] )
= min( 6 + 14, 4 + INFINITY) = 20
D[v2][{v1, v3}] = min( W[2][j] + D[vj][{v1, v3} - {vj}] )
= min( W[2][1] + D[v1][{v3}], W[2][3] + D[v3][{v1}] )
= min( 7 + 10, 8 + 4) = 12
D[v3][{v1, v2}] = min( W[3][j] + D[vj][{v1, v2} - {vj}] )
= min( W[3][1] + D[v1][{v2}], W[3][2] + D[v2][{v1}] )
= min( 3 + INFINITY, INFINITY + 8 ) = INFINITY
k = 3 = n-2 세개 거쳐갈 때
D[v0][{v1, v2, v3}] = min( W[0][j] + D[vj][{v1, v2, v3} - {vj}] )
= min( W[0][1] + D[v1][{v2, v3}],
W[0][2] + D[v2][{v1, v3}],
W[0][3] + D[v3][{v1, v2}] )
= min( 2 + 20, 9 + 12, INFINITY + INFINITY ) = 21
따라서 최단경로는 v0, v2, v3, v1, v0 이고 21
끝..이걸 구현하면 된다. ㅡㅡ;
구현해보자!!!
우선 부분집합을 어떻게 나타낼 것인지 생각해보자
부분집합 표현!!
예를 들어보면 그림 3.16에서
V = { v0, v1, v2, v3 } 는
1, 0001 은 v0
2, 0010 은 v1
4, 0100 은 v2
8, 1000 은 v3
V - {v0} 은 1110로 나타낼 수 있네..
{v0, v2} 은 0101 이구...
for문을 돈다
A = { 모든 부분 집합 }
이건 A (V의 모든 부분집합)
dex / bin / subset
01 0001 {v0}
02 0010 {v1}
03 0011 {v0, v1}
04 0100 {v2}
05 0101 {v0, v2}
06 0110 {v1, v2}
07 0111 {v0, v1, v2}
08 1000 {v3}
09 1001 {v0, v3}
10 1010 {v1, v3}
11 1011 {v0, v1, v3}
12 1100 {v2, v3}
13 1101 {v0, v2, v3}
14 1110 {v1, v2, v3}
15 1111 {v0, v1, v2, v3}
이건 A - {v0}01 0001 {v1}
02 0010 {v2}03 0011 {v1, v2}
04 0100 {v3}05 0101 {v1, v3}06 0110 {v2, v3}07 0111 {v1, v2, v3}
08 1000 {v4}09 1001 {v1, v4}
10 1010 {v2, v4}11 1011 {v1, v2, v4}
12 1100 {v3, v4}13 1101 {v1, v3, v4}14 1110 {v2, v3, v4}15 1111 {v1, v2, v3, v4}
A-{v0}은 짝수다 (v0 즉 0001을 뺏기 때문에 짝수 가 된다)
02 0010 {v1}
04 0100 {v2}
06 0110 {v1, v2}
08 1000 {v3}
10 1010 {v1, v3}
12 1100 {v2, v3}
14 1110 {v1, v2, v3}
....OK?
슬슬 코드를 만들어보자
위 패턴을 보면 대충 for문을 어떻게 할건지 눈에 들어올 것이다.
그럼 위 패턴을 부분집합 표현으로 바꾸어 다시 생각해보자.
D[i][A] = min( W[i][j] + D[vj][A - {vj}] );
int W[4][4] = {
{ 0, 2, 9, INFINITY},
{ 1, 0, 6, 4},
{ INFINITY, 7, 0, 8},
{ 6, 3, INFINITY, 0} };
이 W에서 차근차근 D를 채워나간다.
위 표현을 부분집합으로 바꾸면
아무것도 거쳐가지 않고 갈때
D[1][0] = W[0][1] = 1
D[2][0] = W[0][2] = INFINITY
D[3][0] = W[0][3] = 6
k = 1 하나만 거쳐서 갈 때
D[1][4] = min( W[1][j] + D[vj][{v2} - {vj}] ) = W[1][2] + D[2][0] = 6 + INFINITY
D[1][8] = min( W[1][j] + D[vj][{v3} - {vj}] ) = W[1][3] + D[3][0] = 4 + 6 = 10
D[2][2] = min( W[2][j] + D[vj][{v1} - {vj}] ) = W[2][1] + D[1][0] = 7 + 1 = 8
D[2][8] = min( W[2][j] + D[vj][{v3} - {vj}] ) = W[2][3] + D[3][0] = 8 + 6 = 14
D[3][2] = min( W[3][j] + D[vj][{v1} - {vj}] ) = W[3][1] + D[1][0] = 3 + 1 = 4
D[3][4] = min( W[3][j] + D[vj][{v2} - {vj}] ) = W[3][2] + D[2][0] = INFINITY + INFINITY
k = 2 두개 거쳐갈 때
D[1][12] = min( W[1][j] + D[vj][{v2, v3} - {vj}] )
= min( W[1][2] + D[2][8], W[1][3] + D[3][4] )
= min( 6 + 14, 4 + INFINITY) = 20
D[2][10] = min( W[2][j] + D[vj][{v1, v3} - {vj}] )
= min( W[2][1] + D[1][8], W[2][3] + D[3][2] )
= min( 7 + 10, 8 + 4) = 12
D[3][6] = min( W[3][j] + D[vj][{v1, v2} - {vj}] )
= min( W[3][1] + D[1][4], W[3][2] + D[2][2] )
= min( 3 + INFINITY, INFINITY + 8 ) = INFINITY
k = 3 = n-2 세개 거쳐갈 때
D[0][14]= min( W[0][j] + D[vj][{v1, v2, v3} - {vj}] )
= min( W[0][1] + D[1][12],
W[0][2] + D[2][10],
W[0][3] + D[3][6] )
= min( 2 + 20, 9 + 12, INFINITY + INFINITY ) = 21
배열의 값을 부분집합을 표현으로 0~16까지의 수로 바꾸었다.
배열 D의 내용은 이렇다. (99는 INFINITY)
n = 4
D = [i][pow(2,n)-1]
00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 00, 21
01, 00, 00, 00, 99, 00, 00, 00, 10, 00, 00, 00, 20, 00, 00
99, 00, 08, 00, 00, 00, 00, 00, 14, 00, 12, 00, 00, 00, 00
06, 00, 04, 99, 00, 99, 00, 00, 00, 00, 00, 00, 00, 00, 00
이런 식으로 D의 값들이 들어가 이용된다.
현재 10월 4일 목요일 새벽 4시 40분
이틀동안 코딩하고, 자고, 먹고를 반복한 끝에
다듬어 지진 않았지만
아래와 같은 배열을 얻을 수 있었다...이제 좀 다듬고
입력되는 W를 130쪽 문제5로 바꾸어 해본다음,
brute force 알고리즘으로(recursive)
짜봐야한다.
거의 끝났다...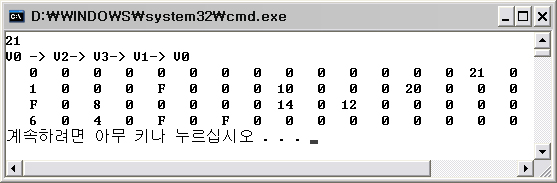
코드가
와~ 완존 스파게티다~
정리정돈좀하고..주석좀 달아야지...
책에 나온 알고리즘대로 하려고 했는데
부분집합을 나타내고 연산하는데서 약간은 loop와 if 가 들어갔다...
최대한 최적화 해야겠따...수동최적화 ㅡㅡ;
상환아 하혁아 잘되냐~~~ㅋㅋㅋㅋㅋ
으흐흐...